精品久久看,欧美成人久久一级c片免费,日本加勒比在线精品视频,国产一区二区三区免费大片天美,国产成人精品999在线,97理论三级九七午夜在线观看

東坡下載：內(nèi)容最豐富最安全的下載站！

幫助|文件類型庫(kù)|最新更新|下載分類|排行榜

工作模板節(jié)日模板老師ppt模板學(xué)生ppt模板慶典模板公開課模板工作報(bào)告工作計(jì)劃動(dòng)態(tài)PPT創(chuàng)業(yè)計(jì)劃勵(lì)志PPT安全教育

首頁(yè) → ppt模板下載 → 老師ppt模板 → 數(shù)學(xué)直線和圓的位置關(guān)系ppt 人教版

數(shù)學(xué)直線和圓的位置關(guān)系ppt

數(shù)學(xué)直線和圓的位置關(guān)系ppt人教版

  • 大小：6.2M
  • 語(yǔ)言：中文
  • 平臺(tái)：WinAll
  • 更新：2019-12-20 14:37
  • 等級(jí)：
  • 類型：老師ppt模板
  • 網(wǎng)站：暫無(wú)
  • 授權(quán)：免費(fèi)軟件
  • 廠商：
  • 產(chǎn)地：國(guó)產(chǎn)軟件
好用好玩 50%(0)
坑爹 坑爹 50%(0)
軟件介紹軟件截圖相關(guān)軟件軟件教程網(wǎng)友評(píng)論下載地址

為大家?guī)?lái)的是數(shù)學(xué)直線和圓的位置關(guān)系ppt，精選多套優(yōu)質(zhì)相關(guān)ppt課件素材，內(nèi)容豐富多樣，講解清晰透徹，可使學(xué)生們學(xué)習(xí)效率更高，歡迎下載使用。

數(shù)學(xué)直線和圓的位置關(guān)系ppt素材

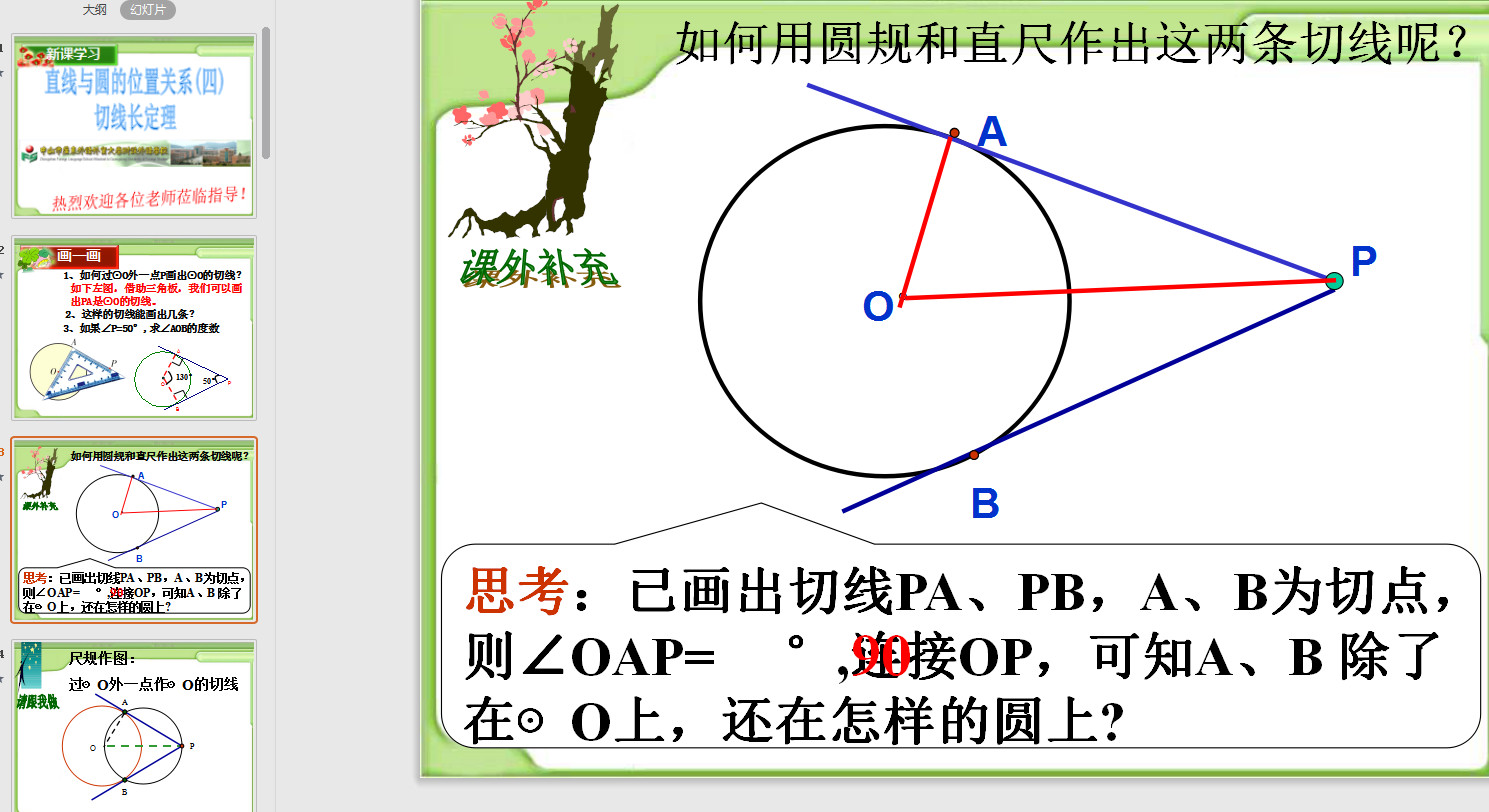
相切

數(shù)學(xué)領(lǐng)域的詞語(yǔ)。直線和圓相切，直線和圓有唯一公共點(diǎn)，叫做直線和圓相切。可以通過比較圓心到直線的距離d與圓半徑r的大小、或者方程組、或者利用切線的定義來(lái)證明。

切線判定定理

切線判斷定理：經(jīng)過半徑外端點(diǎn)并且垂直于這條半徑的直線是圓的切線。

切線的判定方法

【定義】

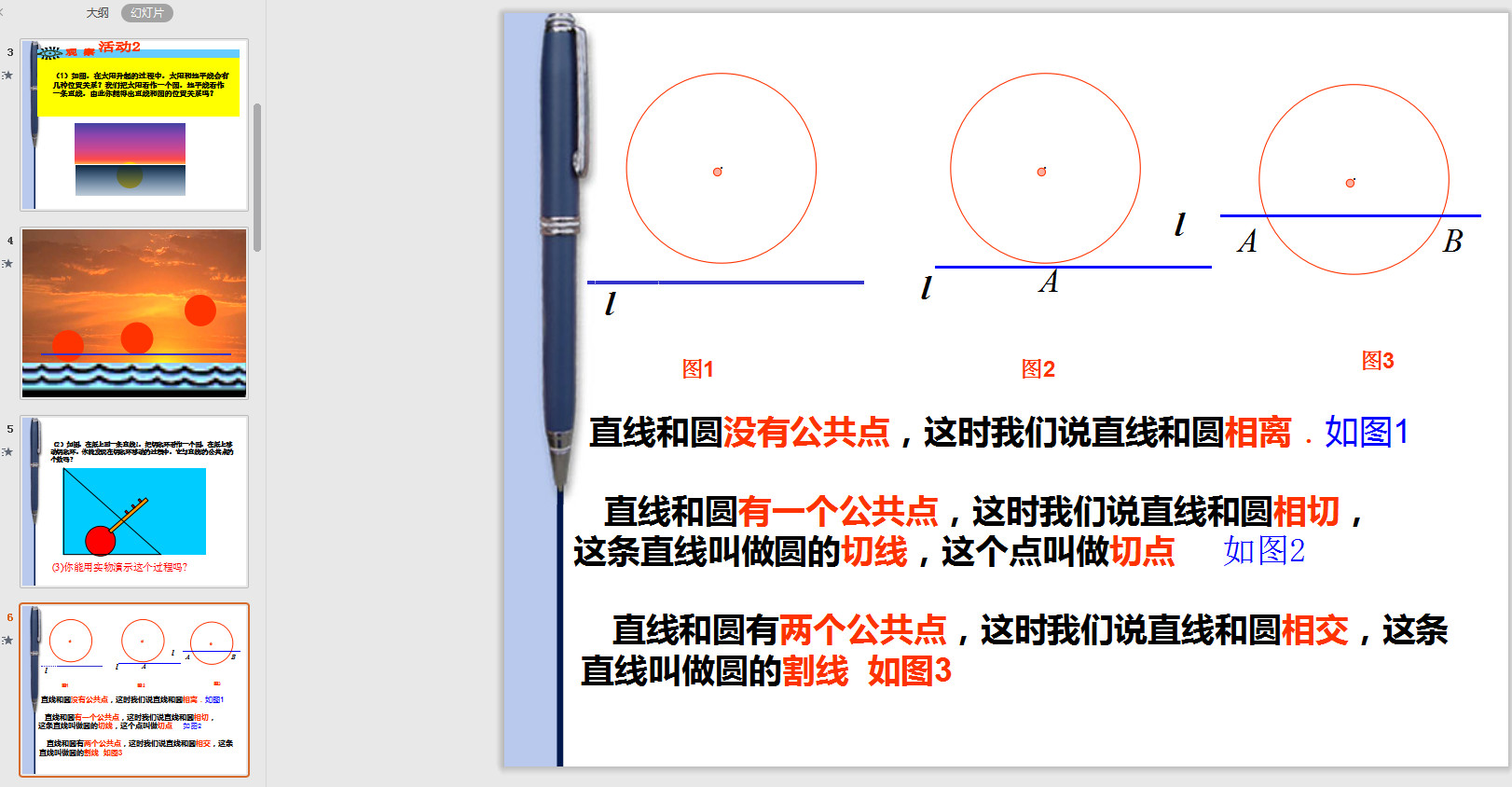
如果直線與圓只有一個(gè)公共點(diǎn)，這時(shí)直線

與圓的位置關(guān)系叫做相切。這條直線叫做圓的切線，這個(gè)公共點(diǎn)叫做切點(diǎn)。

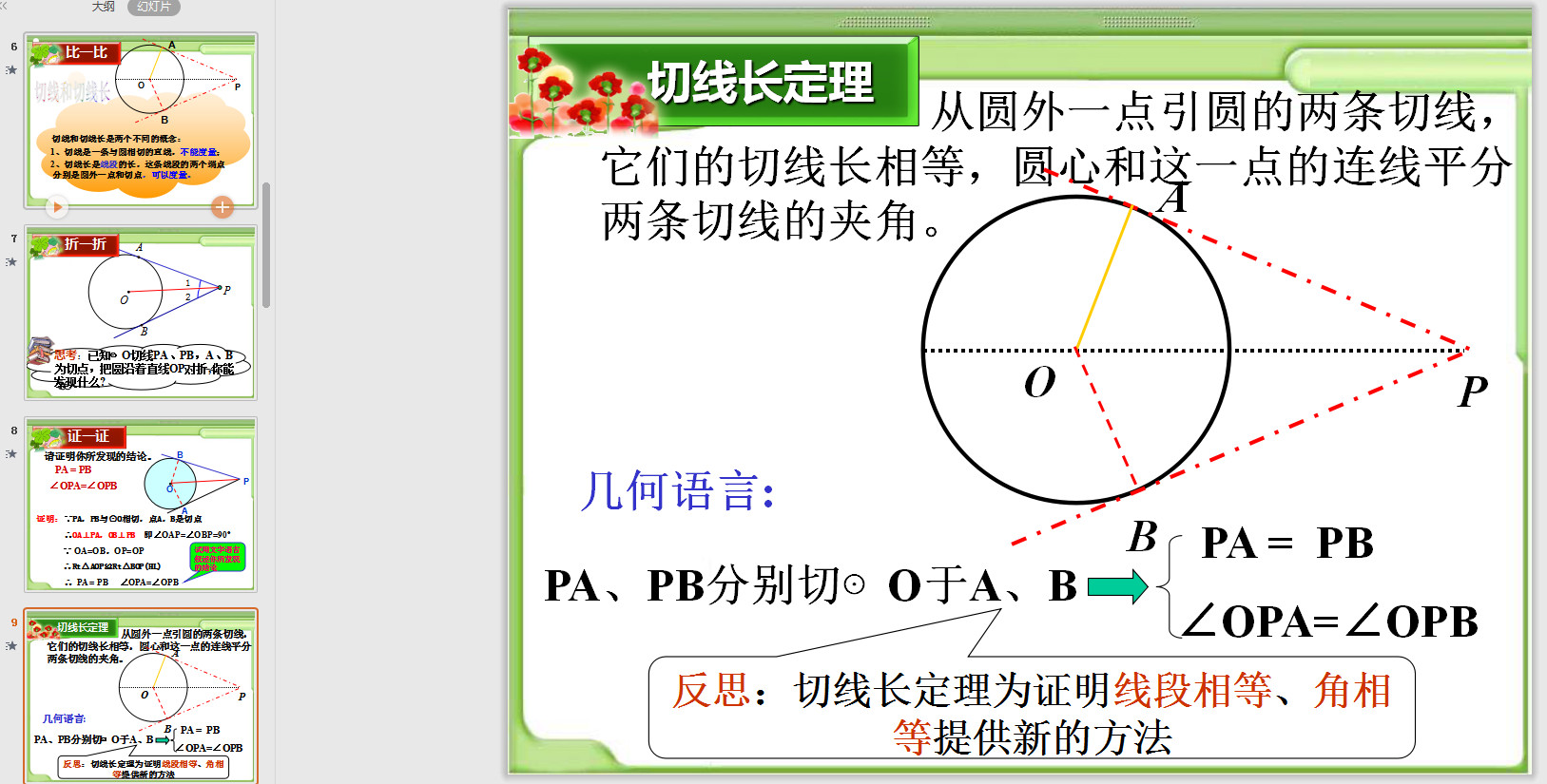
切線性質(zhì)：圓的切線垂直于經(jīng)過切點(diǎn)的半徑。

【證明】

已知：直線l與⊙O有交點(diǎn)A，且OA⊥l ；

求證：l是⊙O的切線。

證明：假設(shè)直線l不是⊙O的切線，

則⊙O與l有兩個(gè)交點(diǎn)，設(shè)另外一個(gè)交點(diǎn)為B，連接OB。

由于A、B都是⊙O上的點(diǎn)，因此OA=OB。又OA⊥l ，由于直角三角形中斜邊大于直角邊，有OA<OB，與OA=OB矛盾；

因此假設(shè)不成立，l是⊙O的切線。

PC官方版
安卓官方手機(jī)版
IOS官方手機(jī)版

數(shù)學(xué)直線和圓的位置關(guān)系ppt截圖

下載地址

數(shù)學(xué)直線和圓的位置關(guān)系ppt 人教版

熱門評(píng)論
最新評(píng)論
發(fā)表評(píng)論 查看所有評(píng)論(0)
昵稱:
表情: 高興 可 汗 我不要 害羞 好 下下下 送花 屎 親親
字?jǐn)?shù): 0/500 (您的評(píng)論需要經(jīng)過審核才能顯示)

本類軟件排行

本類軟件必備

報(bào)錯(cuò)

請(qǐng)簡(jiǎn)要描述您遇到的錯(cuò)誤，我們將盡快予以修正。

轉(zhuǎn)帖到論壇
輪壇轉(zhuǎn)帖HTML方式

輪壇轉(zhuǎn)帖UBB方式

主站蜘蛛池模板： 成人欧美1314www色视频 | 国产91精品一区二区麻豆网站 | 天天夜夜狠狠 | 色偷偷亚洲男人天堂 | 伊人网2021| 国产偷久久 | 国产你懂的在线观看 | 欧美色综合高清免费 | 国产亚洲精品视频中文字幕 | 亚洲精品天堂在线观看 | 欧美亚洲日本国产综合网 | 久久网免费视频 | 国内精品视频一区 | 风流的女兵bd播放 | 国产精品久久久久久 | 国产精品永久免费视频观看 | 日韩免费不卡视频 | 国产精品第一区在线观看 | 第四色播放器 | 国产精品久久久久久久久久一区 | 国产www色| 国产一区二区视频在线观看 | 一级毛片大全免费播放 | 亲爱的妈妈3免费播放中文 亲爱的妈妈3高清hd | 久久久国产视频 | 欧美性视频在线播放 | 免费观看毛片网站 | 久久bb| 婷婷综合五月 | 日韩欧美福利视频 | 四虎成人欧美精品在永久在线 | 天天综合久久久网 | 久久精品中文字幕一区 | 女生宿舍2在线播放 | 日韩国产在线 | 四虎精品成在线播放 | runaway在线观看免费韩国动漫 | 99热4| 激情综合色综合啪啪开心 | 国产精品无码久久久久 | 欧美高清一区二区 |