該初中數學奧林匹克競賽技巧大全主要內容包括特殊的自然講解以及求解問題、數字問題、整除、方程問題講解等,是一份內容十分全面完整的初中數學奧林匹克競賽教程,下載下來之后作為初中數學奧林匹克競賽參考手冊進行查閱使用也是十分不錯的,下文是該數學奧林匹克競賽教程的相關內容介紹,希望對大家有所幫助!
初中數學奧林匹克競賽教程內容節選
……
但這是不可能的,因為k2x2與n2都是完全平方,而由k2<k2+2k<(k+1)2得出k2+2k不是平方數.
A1-003 試證四個連續自然數的乘積加上1的算術平方根仍為自然數.
【題說】 1962年上海市賽高三決賽題 1.
【證】 四個連續自然數的乘積可以表示成
n(n+1)(n+2)(n+3)=(n2+3n)(n2+8n+2)=(n2+3n+1)2-1
因此,四個連續自然數乘積加上1,是一完全平方數,故知本題結論成立.
A1-004 已知各項均為正整數的算術級數,其中一項是完全平方數,證明:此級數一定含有無窮多個完全平方數.
【題說】 1963年全俄數學奧林匹克十年級題2.算術級數有無窮多項.
【證】 設此算術級數公差是 d,且其中一項 a=m2(m∈N).于是
……
【題說】1993年亞太地區數學奧林匹克題4.
【解】顯然,n只能為奇數.
當n=1時,x=-4.
當n為不小于3的奇數時,方程左邊是首項系數為1的非負整系數多項式,常數項是2n+1,所以它的整數解只能具有-2t的形式,其中t為非負整數.若t=0,則x=-1,它不是方程的解;若t=1,則x=-2,也不是方程的解;當t≥2時,方程左邊=2n[-2n(t-1)+(1-2t-1)n+(1+2t-1)n],而-2n(t-1)+(1-2t-1)n+(1+2t-1)n≡2(mod 4),從而方程左邊不等于零.
綜上所述,當且僅當n=1時,原方程有一個整數解x=-4.
A5-033 每一個大于2的自然數n都可以表示為若干個兩兩不等的正整數之和.記這些相加數個數的最大值為A(n),求A(n).
【題說】1993年德國數學奧林匹克(第一輪)題1.
【解】對任意自然數n(n≥3),存在自然數m
……
初中數學奧林匹克競賽教程內容截圖

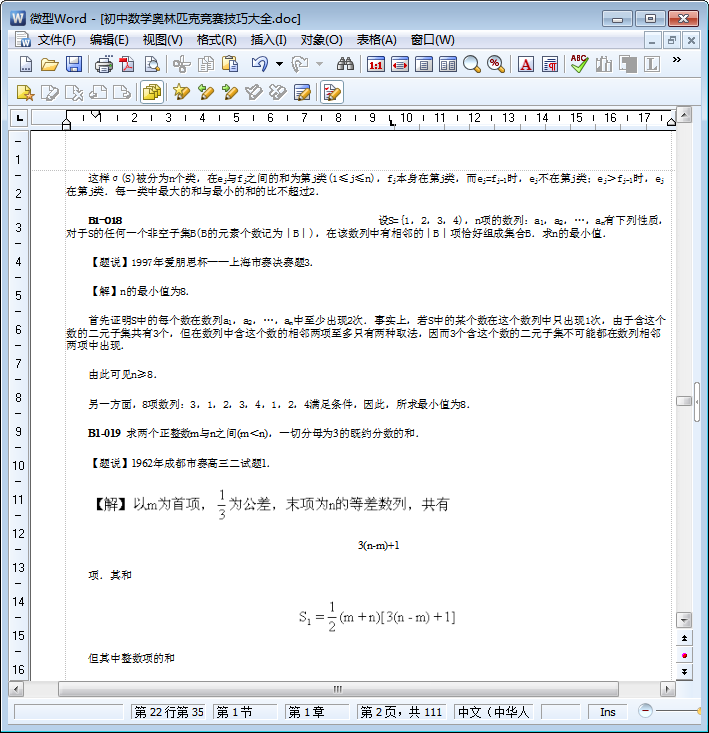
- PC官方版
- 安卓官方手機版
- IOS官方手機版













 DJI 大疆飛行模擬1.4官方版
DJI 大疆飛行模擬1.4官方版
 聯想一鍵禁止驅動更新工具2.26.1 中文綠色版
聯想一鍵禁止驅動更新工具2.26.1 中文綠色版
 關閉硬盤盒自動休眠軟件附教程
關閉硬盤盒自動休眠軟件附教程
 ELM327驅動1.0 官方版
ELM327驅動1.0 官方版
 沃仕達IP Camera CGI應用指南
沃仕達IP Camera CGI應用指南
 PowerPCB電路設計實用教程pdf電子版
PowerPCB電路設計實用教程pdf電子版
 PowerPCB高速電子電路設計與應用pdf高清電子版
PowerPCB高速電子電路設計與應用pdf高清電子版
 電路及電工技術基礎pdf高清電子版
電路及電工技術基礎pdf高清電子版
 硬盤壞道修復教程doc 免費版
硬盤壞道修復教程doc 免費版
 Revit MEP入門教程官方版doc 最新版
Revit MEP入門教程官方版doc 最新版
 新編電腦組裝與硬件維修從入門到精通pdf 高清免費版
新編電腦組裝與硬件維修從入門到精通pdf 高清免費版
 硬件系統工程師寶典pdf免費電子版
硬件系統工程師寶典pdf免費電子版
 xbox one手柄連接電腦教程doc完整免費版
xbox one手柄連接電腦教程doc完整免費版
 硬件工程師入門教程pdf高清免費下載
硬件工程師入門教程pdf高清免費下載
 Hyper-v虛擬機如何訪問USB設備doc完整版
Hyper-v虛擬機如何訪問USB設備doc完整版
 電腦主板跳線的接法詳解doc最新免費版
電腦主板跳線的接法詳解doc最新免費版
 線性穩壓器基礎知識pdf完整版
線性穩壓器基礎知識pdf完整版
 ModelSim簡明使用教程pdf版
ModelSim簡明使用教程pdf版
 數字電子技術基礎教程(閻石第5版)pdf版
數字電子技術基礎教程(閻石第5版)pdf版
 電路第五版邱關源pdf高清免費版
電路第五版邱關源pdf高清免費版
 計算機組成與設計硬件軟件接口第五版pdf附答案完整版
計算機組成與設計硬件軟件接口第五版pdf附答案完整版
 金融煉金術(原版)pdf格式【中文完整版】
金融煉金術(原版)pdf格式【中文完整版】
 深入PHP面向對象模式與實踐(中文第三版)pdf高清掃描版【完整版】
深入PHP面向對象模式與實踐(中文第三版)pdf高清掃描版【完整版】
 HADOOP實戰(中文第二版)pdf清晰完整電子版
HADOOP實戰(中文第二版)pdf清晰完整電子版
 大數據時代 生活工作與思維的大變革pdf中文完整版免費下載
大數據時代 生活工作與思維的大變革pdf中文完整版免費下載
 U盤裝系統(優盤安裝操作系統)圖解教程 PDFpdf完整高清版【附源代碼】免費下載
U盤裝系統(優盤安裝操作系統)圖解教程 PDFpdf完整高清版【附源代碼】免費下載
 機械設計手冊第五版電子版pdf高清免費版
機械設計手冊第五版電子版pdf高清免費版
 證券分析第六版pdf格式高清免費版【完整版】
證券分析第六版pdf格式高清免費版【完整版】
 瘋狂java講義(第3版)pdf (中文版)電子版
瘋狂java講義(第3版)pdf (中文版)電子版





 明朝那些事兒無刪減txt全集下載
明朝那些事兒無刪減txt全集下載 JGJ145-2013混凝土結構后錨固技術規程pdf完
JGJ145-2013混凝土結構后錨固技術規程pdf完 公路養護安全作業規程JTG H30—2015pdf高清
公路養護安全作業規程JTG H30—2015pdf高清 課程表空白表格【免費下載版】
課程表空白表格【免費下載版】 裝配式混凝土結構技術規程JGJ1-2014pdf電子
裝配式混凝土結構技術規程JGJ1-2014pdf電子 混凝土強度檢驗評定標準GB/T50107-2010電子
混凝土強度檢驗評定標準GB/T50107-2010電子 標準視力表高清大圖(A4打印版視力表)bmp格式
標準視力表高清大圖(A4打印版視力表)bmp格式 普通混凝土配合比設計規程JGJ/55-2011pdf電
普通混凝土配合比設計規程JGJ/55-2011pdf電 熱交換器GB/T151-2014pdf電子完整高清版免費
熱交換器GB/T151-2014pdf電子完整高清版免費 鋼筋焊接及驗收規程JGJ18-2012pdf掃描高清版
鋼筋焊接及驗收規程JGJ18-2012pdf掃描高清版